機械学習ではしばしば微分を計算することがあります。Pythonで使える機械学習ライブラリで実装をする場合には、とりわけ微分の知識が必要になることは少ないですが、教養として理解しておくと良いと思います。
ここでは、高校数学で勉強する、「微分」をさらっと学びます。
微分とは?
微分は、ある関数の導関数を求めることを指します。例えば機械学習では、関数の最小化問題を解かなければならない場合があります。ある関数f(x)が最小となるxを探すには、f(x)の導関数を求めなければなりません。このような時に、微分が必要になるのです。
ある関数の微分は、その関数における接線の傾きを意味します。簡単な例として、関数f(x) = x^2の場合を考えます。f(x)のx=4における接線と、f(x)をグラフに表すと、次のようになります。

接線は文字通り関数と接している線です。この接線は基準とするxをどこに設定するかによって傾きが変化します。この傾きは、導関数と一致していることが知られています。したがって、接線の傾きをxの関数として表せば、f(x)の導関数を求めることができそうです。
では、どのようにして接線の傾きをxで表現すれば良いのでしょうか。ここで、関数の2つの点に注目したいと思います。
その2つの点は、(x,f(x))と(x+h,f(x+h))です。hは実数を示しています。
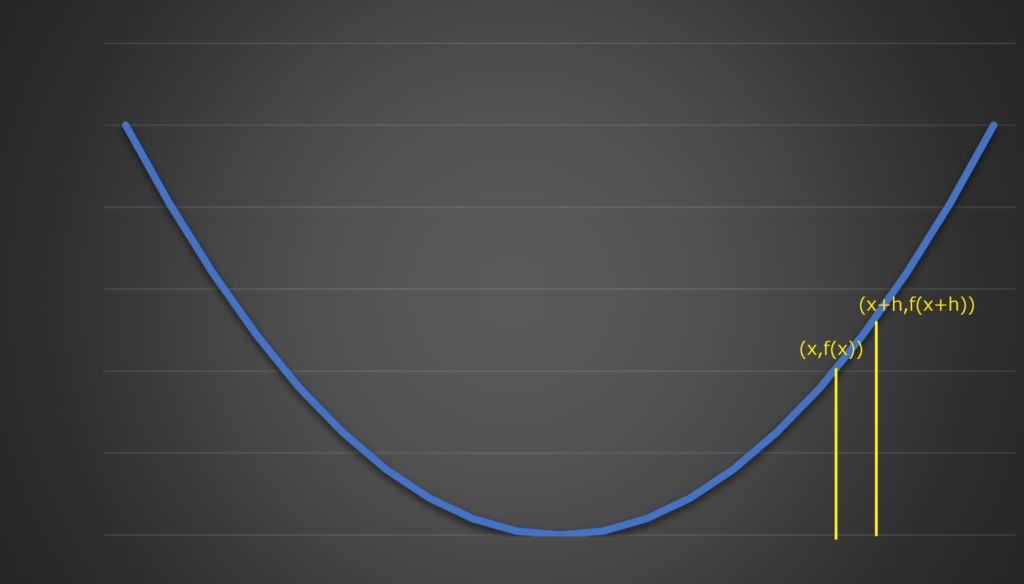
ここで、この2点を通る直線の傾きを計算したいと思います。傾きは、(yの変化量)/(xの変化量)で求められるので、傾き=(f(x+h)-f(x))/hとなります。
この傾きの式は、xとhの2つの文字で表されています。これをxだけの式にするには、hを消せば良さそうです。
hをひたすら0に近づけていくと、2点間の距離は狭まり、やがて1つの点に収束します。つまり、先ほどの傾きの式でhを0に近づけた際の極限を求めればf'(x)をxの関数として導出することができます。
これより、微分の定義を示す式が導出されます。ある関数f(x)の導関数f'(x)は、次のような式で表すことができます。
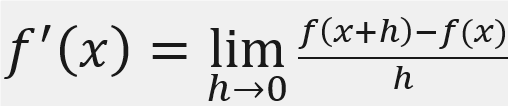
微分の定義式から導関数を計算する
先ほど求めた式を使って、導関数を計算したいと思います。
例:f(x) = x^2の場合
f'(x) = (x+h)^2 – x^2/h = (x^2 + 2hx + h^2 – x^2)/h = ( h^2 + 2hx)/h = h + 2x → 2x
簡単に計算できました。関数f(x) = x^2の導関数は2xです。
微分の公式
ここで、f(x) = x^n(nは実数)と表される関数の導関数を求める公式を紹介します。

これを覚えておけば、一瞬で導関数を計算することができます。
例1$$f(x)= x^3$$
$$f'(x) = 3x^2$$
例2 $$ f(x) = x^5 $$
$$ f'(x) = 5x^4 $$
今回は、微分の定義を紹介し、簡単な関数を微分する方法を学習しました。次回の「機械学習と数学」では、三角関数や対数の微分を学びます。

